METROPOLIS2 Course

Session 3: Demand Side

Lucas Javaudin

Spring 2024

Questions regarding last Session?

Plan of this Session

  1. Introduction
  2. Mode Choice
  3. Road and Virtual Trips
  4. Departure-Time Choice
  5. Advanced Demand Modeling
  6. Task for Next Session

Introduction

Sessions

  1. Introduction (13th March)
  2. Supply side: road network (27th March)
  3. Demand side: agents, travel alternatives and trips (3rd April)
  4. Technical parameters and running the simulator (10th April)
  5. Reading and understanding the results (17th April)
  6. Case-study: Paris' low-emission zone (Input)
  7. Case-study: Paris' low-emission zone (Output)
  8. Extensions: fuel consumption, CO2 emissions and local pollutants

METROPOLIS2 Fundamental Flow Diagram

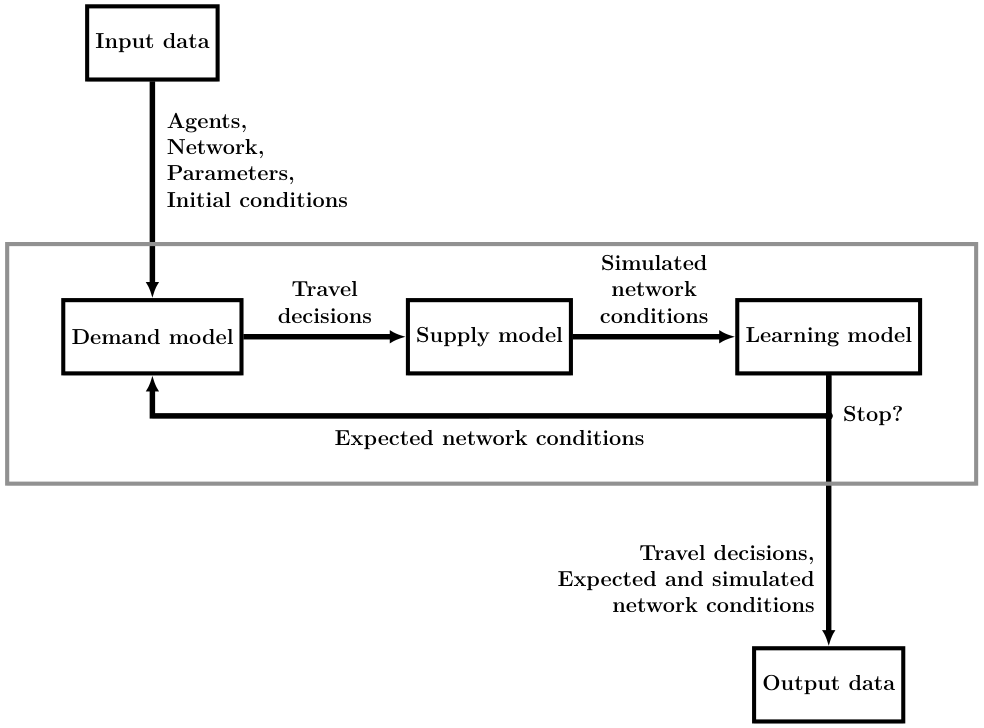
METROPOLIS2 Input Files

  • Parameters (JSON)
  • Supply side:
    • Road network (Parquet or CSV)
    • Vehicle types (Parquet or CSV)
  • Demand side:
    • Agents (Parquet or CSV)
    • Travel alternatives (Parquet or CSV)
    • Trips (Parquet or CSV)
  • Optional road-network conditions (Parquet or CSV)

Documentation

For additional details and references on what is covered during this session, refer to the documentation

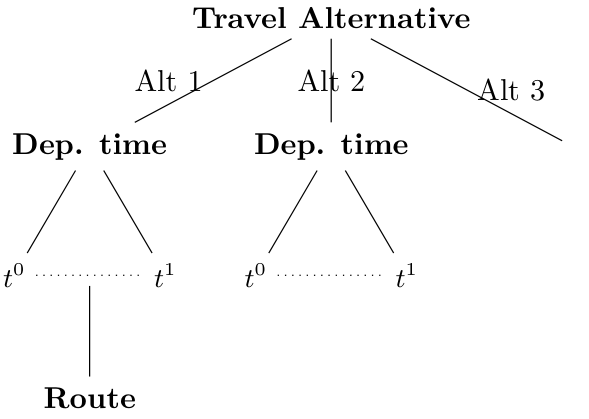
https://docs.metropolis.lucasjavaudin.com/getting_started/input/agents.html

METROPOLIS2 Decision Tree

  • Level 1: choice between travel alternatives
  • Level 2: choice of a departure time (except for no-trip alternatives)
  • Level 3: choice of a route (for road trips only)

Parameters JSON File for this Session

To run the example simulations of this session, create the following parameters.json file: 

					{
						"input_files": {
							"agents": "agents.csv",
							"alternatives": "alts.csv"
						},
						"output_directory": "output",
						"max_iterations": 1,
						"period": [0.0, 3600.0],
						"saving_format": "CSV"
					}

Mode Choice

Travel Alternatives

  • Travel alternative: description of a plan / program / strategy that the agent can choose to execute
  • Examples: travel from home to work by car; travel from home to work by public-transit then from work to shop by walking; do not travel
  • All agents must have at least one alternative
  • At each iteration, each agent is selecting exactly one alternative to execute
  • In most cases, the choice of an alternative represents a mode choice

Run 1: No Mode Choice, No Utility

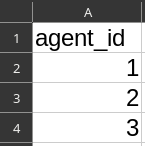
  • File agents.csv:

    • Column agent_id = 1,2,3

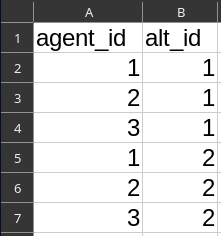
    File alts.csv

    • Column agent_id = 1,2,3
    • Column alt_id = 1,1,1,2,2,2
  • Run METROPOLIS2
  • Read the output file agent_results.csv

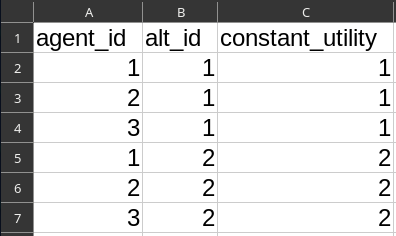
Run 2: Constant Utility

  • File alts.csv

    • Column constant_utility = 1,1,1,2,2,2
  • Run METROPOLIS2
  • Read the output file agent_results.csv
    When no mode choice (= alternative choice) is specified, the first alternative is always the chosen one.

Run 3: Deterministic Mode Choice

  • File agents.csv

    • Column alt_choice.type = Deterministic
  • Run METROPOLIS2
  • Read the output file agent_results.csv
    All agents are choosing alternative 2 and get 2 utility units

Logit Model

  • Consider an agent choosing between two alternatives 1 and 2
  • (Deterministic) utility of alternative 1 (resp. 2) is $V_1$ (resp. $V_2$)
  • Discrete-choice theory: total utility of alternative $j$ is \[ U_j = V_j + \varepsilon_j \]
  • Logit model if $\varepsilon_j \overset{i.i.d.}{\sim} \textit{Gumbel}$
  • Probability to choose alternative $1$ is \[ p_1 = \text{Prob}(U_1 > U_2) = \frac{e^{V_1}}{e^{V_1} + e^{V_2}} \]
  • Expected utility from the choice \[ \mathbb{E}_{\varepsilon}[\max_j U_j] = \ln(e^{V_1} + e^{V_2}) + 0.577 \]

Multinomial Logit and Continuous Logit

Multinomial Logit
  • Probability to choose alternative $j$: \[ p_j = \frac{e^{V_j / \mu}}{\sum_k e^{V_k / \mu}} \]
  • Expected utility from the choice \[ \mathbb{E}_{\varepsilon}[\max_j U_j] = \mu \ln \sum_j e^{V_j / \mu} + \mu \cdot 0.577 \]
Continuous Logit
  • Probability to choose interval $[t, t']$: \[ p([t, t']) = \frac{\int_{t}^{t'} e^{V(\tau) / \mu} \text{d} \tau}{\int_{t^0}^{t^1} e^{V(\tau) / \mu} \text{d} \tau} \]
  • Expected utility from the choice \[ \mathbb{E}_{\varepsilon}[\max_\tau U(\tau)] = \mu \ln \int_{t^0}^{t^1} e^{V(\tau) / \mu} \text{d} \tau + \mu \cdot 0.577 \]

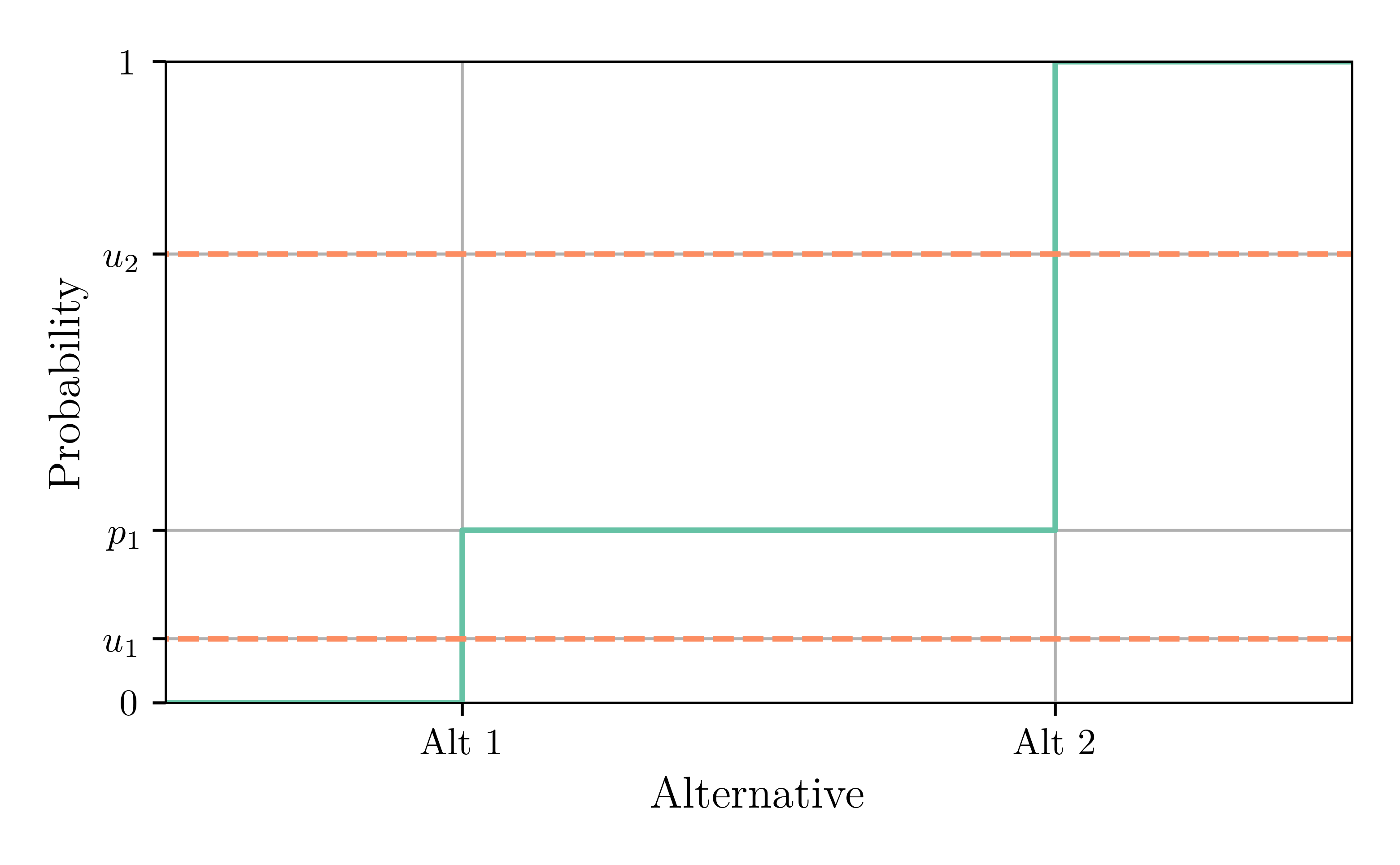
Inverse Transform Sampling

  1. Draw a value $u_n \sim \text{Uniform}([0, 1])$ for each agent
  2. Select alternative 1 if $u_n < p_1$

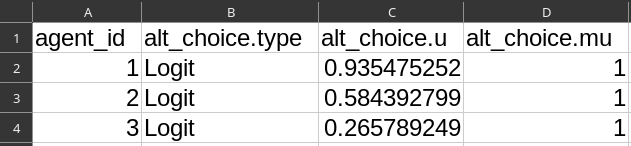
Run 4: Logit Mode Choice

  • File agents.csv

    • Column alt_choice.type = Logit
    • Column alt_choice.u = RAND()
    • Column alt_choice.mu = 1
  • Run METROPOLIS2
  • Read the output file agent_results.csv

Virtual Trips

Overview

  • Each alternative consists in 0, 1 or more trip(s), to be executed sequentially
  • Two types of trips: road and virtual
  • Road trip: origin, destination, vehicle type (will be covered during Session 4)
  • Virtual trip (or teleport trip): exogenous travel time (e.g., walking, cycling, public transit)

Parameters JSON File

Add the "trips.csv" file to the parameters 

					{
						"input_files": {
							"agents": "agents.csv",
							"alternatives": "alts.csv",
							"trips": "trips.csv"
						},
						"output_directory": "output",
						"max_iterations": 1,
						"period": [0.0, 3600.0],
						"saving_format": "CSV"
					}

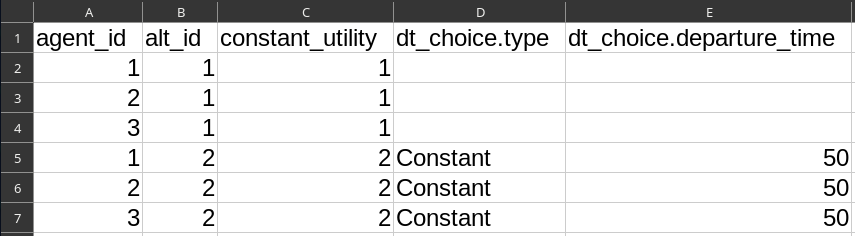
Run 5: Virtual Trip

  • File alts.csv:

    • Column dt_choice.type = Constant
    • Column dt_choice.departure_time = 50

    File trips.csv:

    • Column agent_id = 1,2,3
    • Column alt_id = 2,2,2
    • Column trip_id = 1,1,1
    • Column class.type = Virtual
    • Column class.travel_time = 100
  • Run METROPOLIS2
  • Read the output file agent_results.csv

Travel Utility

  • Utility of a no-trip alternative is simply equal to constant_utility
  • Utility of an alternative with a single trip is equal to \[ \text{utility} = \texttt{constant\_utility} + \texttt{travel\_utility.one} \times \text{travel\_time} \]
  • Variables travel_utility.two, travel_utility.three and travel_utility.four can be use for a polynom of up to degree 4
  • Schedule-delay utility can also be added (to be seen in the next part)

Run 6: Travel Utility

  • File trips.csv:

    • Column travel_utility.one = -0.01,-0.01,-0.01
  • Run METROPOLIS2
  • Read the output file agent_results.csv
    Read the output file trip_results.csv

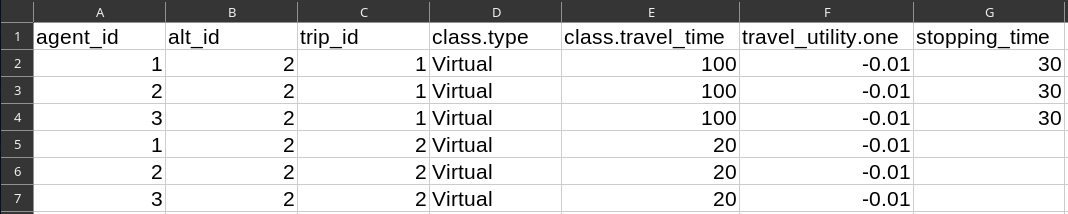
Trip Chaining

  • Each alternative can contain an arbitrary number of trips (a mix of road and virtual trips is possible)
  • The trips are performed in the order in which they appear in the trips input file
  • The stopping_time variable can be used to add a delay between two trips (this can represent the activity duration)

Run 7: Trip Chaining

  • File trips.csv:

    • Column agent_id = 1,2,3,1,2,3
    • Column alt_id = 2,2,2,2,2,2
    • Column trip_id = 1,1,1,2,2,2
    • Column class.type = Virtual
    • Column class.travel_time = 100,100,100,20,20,20
    • Column travel_utility.one = -0.01
    • Column stopping_time = 30,30,30,,,
  • Run METROPOLIS2
  • Read the output files agent_results.csv and trip_results.csv

Departure-Time Choice

Overview

  • Three types of departure-time approaches: Constant (dynamic traffic assignment), Continuous choice (Continuous Logit model), Discrete choice
  • The only decision variable for departure-time choice is the departure time for the first trip of the trip chain → the departure time for the subsequent trips depends of the previous' trips travel times and stopping times
  • The departure-time choice is based on the (anticipated) utility for the entire trip chain

Continuous Logit

  • Probability to choose interval $[t, t']$: \[ p([t, t']) = \frac{\int_{t}^{t'} e^{V(\tau) / \mu} \text{d} \tau}{\int_{t^0}^{t^1} e^{V(\tau) / \mu} \text{d} \tau} \]
  • Expected utility from the choice \[ \mathbb{E}_{\varepsilon}[\max_\tau U(\tau)] = \mu \ln \int_{t^0}^{t^1} e^{V(\tau) / \mu} \text{d} \tau + \mu \cdot 0.577 \]
With a constant utility function ($V(\tau) = \bar{V}$):
  • Probability to choose interval $[t, t']$: \[ p([t, t']) = \frac{t' - t}{t^1 - t^0} \]
  • Expected utility from the choice \[ \mathbb{E}_{\varepsilon}[\max_\tau U(\tau)] = \bar{V} + \mu \cdot \ln(t^1 - t^0) + \mu \cdot 0.577 \]

Run 8: Continuous Departure-Time Choice

  • File alts.csv:

    • Column dt_choice.type = Continuous
    • Column dt_choice.model.type = Logit
    • Column dt_choice.model.u = RAND()
    • Column dt_choice.model.mu = 1
  • Run METROPOLIS2
  • Read the output files agent_results.csv

Expected Utility vs Alt Expected Utility vs Utility

  • utility: Simulated utility, based on the selected alternative $j$ and departure time $\tau$: $V^{\text{sim}}_{j}(\tau)$
  • alt_expected_utility: Expected utility of the departure-time choice of the selected alternative $j$: $\mathbb{E}_{\varepsilon}[\max_{\tau} U_j(\tau)]$
  • expected_utility: Expected utility of the alternative choice: $\mathbb{E}_{\varepsilon}[\max_{j} U_j]$

Utility

  • Utility of a trip is \[ \text{trip utility} = \text{travel utility} + \text{schedule utility} \] with \[ \text{travel utility} = \texttt{travel\_utility.one} \times {tt} \] and \[ \text{schedule utility} = -\texttt{beta} \times [\texttt{tstar} - t^a]_+ - \texttt{gamma} \times [t^a - \texttt{tstar}]_+ \]
  • Total utility of a travel alternative is \[ \text{utility} = \texttt{constant\_utility} + \sum_{\text{trip}} \text{trip utility} \]

Run 9: Schedule-Delay Utility

  • File trips.csv:

    • Column schedule_utility.type = AlphaBetaGamma
    • Column schedule_utility.tstar = 1800
    • Column schedule_utility.beta = 0.005
    • Column schedule_utility.gamma = 0.02
  • Run METROPOLIS2
  • Read the output file trip_results.csv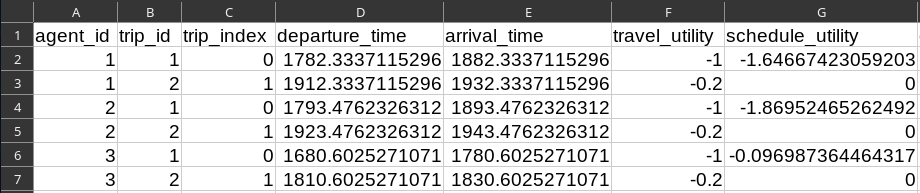

Advanced Demand Modeling

Alternative Choice

  • At the top level, agents choose among an arbitrary number of travel alternatives
  • A travel alternative is defined as a sequence of trips and a utility function specification
  • The alternative choice can represent:
    1. Mode choice: H→W by car | H→W by PT | H→W by walk
    2. Mode choice with trip chaining: H→W→S→H by car | H→W→S→H by bicycle
    3. To travel or not to travel: H→W by car | No trip (work-from-home)
    4. Inter-modality: H→P by car then P→W by PT | H→W by car
    5. Destination choice: H→S1 by walk | H→S2 by walk
    6. Vehicle choice: H→W with a fast but energy-consuming car | H→W with a fuel-efficient but slow car
Legend. H: Home; W: Work; S: Shop; S1: Shop 1; S2: Shop 2; P: Parking lot; PT: Public transit

Choice Models

  • Alternative choice: Multinomial Logit or Deterministic
  • Departure-time choice: Continuous Logit or Multinomial Logit
  • Almost any discrete-choice model is feasible by drawing the epsilon values (idiosyncratic chocs) "offline" and specifying them in the utility
  • Selecting alternative $A$ with probability $p = e^{V_a} / (e^{V_a} + e^{V_b})$ using inverse transform sampling is equivalent to selecting alternative $A$ if and only if $V_A + \varepsilon_A > V_B + \varepsilon_B$ where $\varepsilon_A$ and $\varepsilon_B$ are two Gumbel-distributed values
  • Example for a Probit mode choice with three alternatives:
    1. Draw $\varepsilon_j \sim \mathcal{N}(0, 1), j \in \{1, 2, 3\}$
    2. Add $\varepsilon_j$ to the utility of alternative $j$ in the simulator
    3. Select a deterministic choice model (the value maximizing $V_j + \varepsilon_j$ is selected)

Input data

Two main ways to generate population data:
  • Origin-Destination Matrix: For any row $i$ and colomun $j$ in the matrix, generate $a_{ij}$ agents with a single trip from origin $i$ to destination $j$
  • Synthetic Population:
    • Given various data (census, travel survey, etc.), the synthetic population algorithm returns a list of agents and the activities they perform
    • Easily convertible to METROPOLIS2 input format
    • Travel times for virtual trips can be computed using METROPOLIS2's routing algorithm (See Session 2)
    • Example for France: Hörl, S. and M. Balac (2021) Synthetic population and travel demand for Paris and Île-de-France based on open and publicly available data, Transportation Research Part C

Task for Next Session

Session 3 Task

Create your own population of agents using various features presented in this session (alternative choice, no-trip alternatives, virtual trips, trip chaining, schedule utility, departure-time choice, etc.)